Math 216 Demonstrations

Model Description

Lead has been and continues to be a component in a large number of objects in our environment, perhaps most conspicuously in paints made before 1978 (at which point the US Consumer Product Safety Commission banned lead from paint).[1] It also causes, especially for children, nervous system damage, stunted growth, kidney damage, and delayed development.[2] Lead intake into the body may be through inhalation of lead dust or ingestion; in either case, it ends up in the bloodstream and from there may move into the tissues and bones. This behavior is captured by a three-compartment model, as shown below.

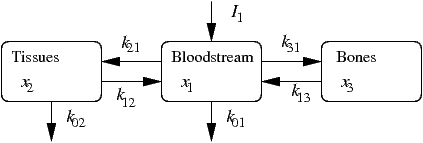
Here lead enters the bloodstream at a rate \(I\), resulting in amounts \(x_1\), \(x_2\) and \(x_3\) in the bloodstream, tissues and bones, and is transferred to compartment \(i\) from compartment \(j\) at a rate \(k_{ij}\). Lead is filtered out of the bloodstream by the kidneys and lost from the tissues into the hair and through tissue loss.

ODE Model

Assuming that all transfers between and out of the compartments indicated above are proportional to the amount of the lead present there as suggested above, we obtain the simple linear system \[ \begin{aligned} x_1'(t) &= -(k_{01} + k_{21} + k_{31})\, x_1(t) + k_{12}\,x_2(t) + k_{13}\,x_3(t) + I_1\\ x_2'(t) &= k_{21}\,x_1(t) - (k_{02} + k_{12})\, x_2(t)\\ x_3'(t) &= k_{31}\,x_1(t) - k_{13}\,x_3(t). \end{aligned} \] with initial condition \(x_1(0) = I_{01}\), \(x_2(0) = I_{02}\) and \(x_3(0) = I_{03}\).

This model was considered in [3] and expanded on in [4], and is described in [5]. In those a controlled experiment in which lead was introduced into a male volunteer's diet and the amount in his bloodstream, tissues and bones considered; from those data, they deduced the values \[ I_1 = 49.3, k_{01} = 0.0211, k_{21} = 0.0111, k_{31} = 0.0039, k_{02} = 0.0162, k_{12} = 0.0124, \quad\mbox{and}\quad k_{13} = 0.000035. \] (values are from [4]; \(I_1\) is in \(\mu\)g/day). For initial conditions we consider all of \(I_{01}\), \(I_{02}\) and \(I_{03}\) to be zero.

Matlab Demos

We consider here a simple demo that graphs a solution to this using Euler's method.

• Lead_Euler.m: A demonstration that graphs the approximate solution to the system generated by Euler's method. Because the time for the third compartment (\(x_3\)) to reach equilibrium, the demonstration plots the solution for a short range of \(t\)-values (given by the parameter t_max_first_graph), pauses, and then graphs the solution for larger times. This is indicated in the configuration section of the demonstration. [show figure]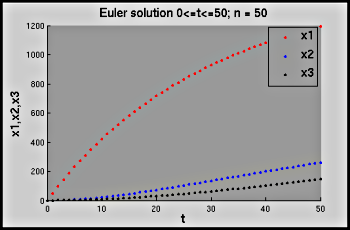
  
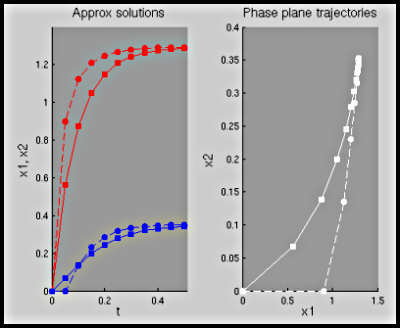
• Lead_Two_Compartment.m: A demonstration that uses the two-compartment lead model (by dropping the bone compartment, rescaling time to be in years and tweaking parameters slightly) to show Euler's and the improved Euler approximations to a system of two equations. Parameters determining the behavior of the demo include h, the step-size, constrain_axis1, show_phase_plane, and include_pauses. These are indicated in the configuration section of the demonstration. By default, if h is larger than 0.1, only the two numerical methods are shown. If h is less than or equal to 0.1, the solution trajectory is also plotted in the phase plane as well (unless show_phase_plane is set to 0). [show figure] (no phase plane)
  
  [show figure] (with phase plane)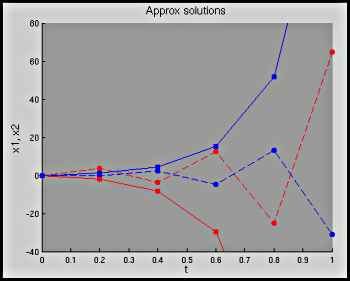
  

Looking at the Model

Some questions that may be worth considering:

• Why is the time to equilibrium so much longer for \(x_3\) than for the other compartments?
• How do we find the equilibrium solutions?

References

1. U.S. Consumer Product Safety Commission (September 1977). "News from the CPSC." CPSC Announces Final Ban On Lead-Containing Paint. USCPSC. Retrieved on: 22 Oct, 2012.
2. Agency for Toxic Substances and Disease Registry (August 2007). ToxFAQs for Lead. Center for Disease Control. Retrieved on: 22 Oct, 2012.
3. Rabinovitz, M.B., Wetherill, G.W., and J.D. Kopple (November 1973). "Lead Metabolism in the Normal Human: Stable Isotope Studies." Science. 182(4113): 725-727.
4. Batschelet, E., Brand, L. and A. Steiner (1979). "On the Kinetics of Lead in the Human Body." Journal of Mathematical Biology 8:15-23.
5. Borelli, R.L. and C.S. Coleman. Differential Equations, a Modeling Perspective, 2nd ed. New York:Wiley, 2004.