Abstract
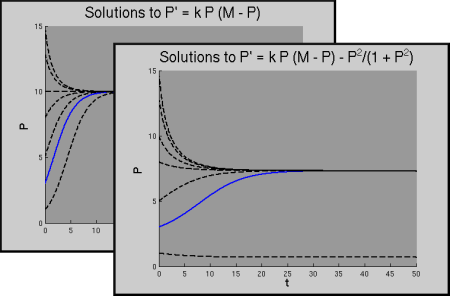
Our approach to population modeling is to take \(P' = \mbox{births} - \mbox{deaths}\). In this case we consider two cases. The first is the standard logistic model, in which \(\mbox{births}\) is modeled by an environmentally limited birth rate, \(\beta(t) = a - b\,P\) so that we have \[ P' = k P (M - P). \] And the second is a situation in which a "non-standard" model for the deaths term is appropriate, a model for the population of the spruce budworm (see also the spruce budworm demos), \[ P' = k P (M - P) - \frac{P^2}{1 + P^2}. \] The resulting differential equations are autonomous and first-order, and therefore separable, but separation may or may not provide useful information about solutions. Here we look at numerical solutions to see what the solutions do, and how the second equation has some interesting behavior not seen in the first.
Use Cases
Lecture: The graph of the solutions to the logistic model illustrates the existence of the long term limiting population. The graph of solutions to the budworm model illustrates a similar behavior, plus the existence of some other interesting behavior for smaller values of \(P\). Because this model is not readily solved this motivates the use of qualitative methods for first-order problems.
Outside of Lecture: Look at the solution curves and make sure that you can see what they tell you about the initial values of the population. What is the value of \(M\) that is used for the logistic equation? How do you know? Note that it is not straightforward to solve the budworm model; can you see how you might find the possible limiting values of the population?
Model Description
The spruce budworm model is described in the documentation for those demos. The logistic model is derived in the usual manner: we assume that \[ P' = \mbox{births} - \mbox{deaths} = \beta(t) P - \delta(t) P, \] where \(\beta\) and \(\delta\) are the birth and death rates per individual in the population. For the logistic equation we let \(\beta = a - b P\) and \(\delta = d\).
ODE Model
Using the birth and death rates above, we obtain the logistic equation \[ P' = k P (M - P). \] Similarly, with \(P\) being a measure of the budworm population (in this case, a scaled population density), we have after rearranging \[ P' = k P (M - P) - \frac{P^2}{1 + P^2}. \] The term \(\frac{P^2}{1 + P^2}\) is a model for (avian) predation.
Matlab Demos
A demo to graph solutions
- Logistic_Budworm.m:
Graphs the solution to the logistic with a given initial condition,
pauses, then adds solutions for other initial conditions, pauses,
and then does the same in a new graph window for the budworm model.
[show
figure]