Abstract
The standard mixing problem is that of a well-mixed saline solution in a tank. A different take on this is a well-shaken box with black balls inserted in through a hole on one side and which bounce out of a hole on the other side. Modeling the number of balls in the box gives a standard first-order, linear ordinary differential equation characteristic of mixing problems, \( N'(t) = a - k N(t) \), which we can solve using integrating factors. Here we can also compare with a discrete simulation of the situation to see how the continuous model compares with the discrete interpretation of the system.
Use Cases
Lecture: The problem may be stated with essentially the same derivation as a standard mixing problem. The demonstrations then show the solution to the problem, found with integrating factors, and reflect on the validity of the model.
Outside of Lecture: Be sure that the derivation of the model is clear, and that you could derive it given the model description. Carefully solve the differential equation using integrating factors, and see that your solution matches that shown in the demonstrations here.
Model Description
Suppose we have a box with a given volume, say \(V = 100\) cubic centimeters, that has a hole in the bottom and in the top. Initially the box is empty, but every second we push some number of black balls (each approximately 1 cubic centimeter large) in through the hole in the bottom (say, \(n = 3\) black balls), and, covering up that hole, shake the box well. Any ball that hits the hole in the top of the box (which we'll say has size \(h = 4\): it is large enough for four balls to exit) will leave the box. Over time, what happens to the number of balls in the box? This is what we model here.
ODE Model
Let \(N(t)\) be the number of black balls in the box. If we assume that the number of balls in the box is sufficiently large that we can measure \(N\) in hundreds or thousands it makes sense to consider fractional values of \(N\) and we can approximate the discrete system with a continuous model. Let \(n\) be the number of balls added to the box each time interval, \(V\) be the box's volume, and \(h\) the exit hole size (in ball-size units). Then we have \[\begin{aligned} \frac{dN}{dt} &= (\mbox{number in each second}) - (\mbox{number out each second}).\\ &= n - h\,(\mbox{fraction of volume occupied by balls})\\ &= n - h\,\frac{N}{V}. \end{aligned} \] Obviously, with \(V = 100\) and \(n = 3\) it might be a bit of a stretch to consider the continuous model to be a good approximation for what's going on in the box, but that's something we can investigate here.
It is worth explitly noting that this formulation is exactly the same as for a more standard mixing problem, with "fraction of volume occupied by balls" being exactly the same as "concentration" in a more standard problem. Then both input and output terms have the form \((\mbox{volume in})(\mbox{concentration})\) (where for the input in this case the concentration is 1 (100%)).
Matlab Demos
We consider a number of Matlab demos for this:
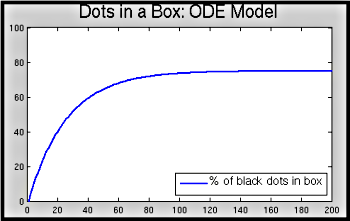
- Example_Mixing_Continuous.m:
A very simple demo that numerically solves the ODE and plots the
solution to show the fraction of black balls in the box.
[show
figure]
[code notes]
- Example_Mixing_Discrete.m:
A very simple demo that simulates the number of balls in the box by
randomly determining at each step which have left the box, and then
plots the resulting fraction of black balls against time.
[show
figure]
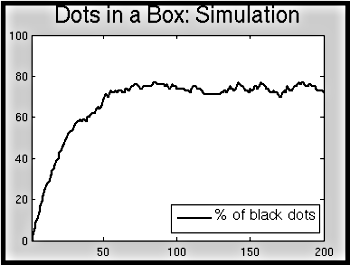
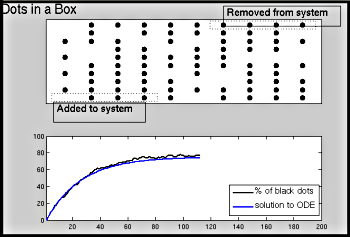
- Example_Mixing_Problem.m:
A demo drawing the box and balls, animating a simulation of the
balls in the box and graph of the corresponding number of balls
along with the solution to the ODE Model.
[show
figure]
Looking at the Model
Some questions that may be worth considering:
- What is the number of balls to begin with in the tank that would remain constant? (This looks forward to chapter 2 and beyond, when we consider stability.)
- What should the size of the top hole be if we want the system to end up with some specified number of balls, e.g., \(N = 50\)?
- Similarly, what should the volume of the box be to make the system end up with some specified number of balls, e.g., \(N = 50\)?
- What will the solution look like if we start with \(N=90\) or \(N=100\) black balls in the box?
