Abstract
We consider a simple model for the velocity of a sprinter in a short sprint, which posits a maximum attainable velocity and that the sprinter's acceleration is proportional to the difference between her/his current speed and that maximum. This gives \( v' = a_0 - k v \), where \( a_0 \) is the maximum acceleration and \( k \) the constant of proportionality. Solutions to this may be obtained, or tested by substitution.
Use Cases
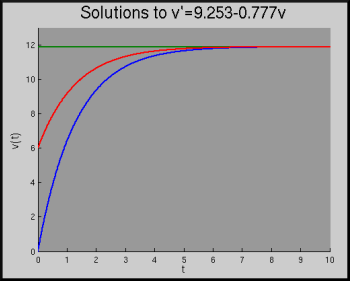
Lecture: The model may be stated with essentially no derivation. It has two easy solutions that students can check by substitution, \(v = a_0/k \) and the expected exponential. The demonstration just graphs the expected solution having \(v(0) = 0\), the equilibrium solution, and one other solution.
Outside of Lecture: Check that you can show that the solutions given below (\(v = 12.11\) and \(v = 12.11 + C e^{-0.721t}\)) do in fact solve the differential equation. Verify that the graphs obtained with the demonstration make sense, and that you can pick out which two of the solutions graphed match these two.
Model Description
Joseph Keller [1] proposed that track sprints up to 300 meters can be described by the equation \[ \frac{dv}{dt} = A - \frac{v}{\tau}, \] in which \(v\) is the sprinter's velocity, \(A\) is the sprinter's initial (maximum) acceleration, and \(\tau\) is a measure of the rate at which the sprinter tires. The model is additionally described in [2], [3], and [4], with a summary for use in a differential equations course appearing in [5].
ODE Model
We seek to model Usain Bolt's (then) world-record 100 meter run of 9.69 seconds in the 2008 Beijing Olympics. With some assumptions, we obtain the model \[ v'(t) = 8.730 - 0.721 v(t) \] (for parameter generation, see [7]).
For any standard race, we have \(v(0) = 0\). If we ignore this and start by looking for a constant solution, we find \(v = 12.11\); solving (with integrating factors) gives the one-parameter family of solutions \(v = 12.11 + C e^{-0.721t}\).
Matlab Demos
The demo here graphs the solutions \(v = 12.11 (1 - e^{-0.721t})\), which solves the initial value problem, the constant solution \(v = 12.11\), and a third solution in the family of solutions to the differential equation that has \(v(0) = 6\).
- Sprinter.m:
Graphs the three solutions indicated.
[show
figure]
References
- Keller, J.B. A Theory of Competitive Running. Physics Today Sep 1973, p.43.
- Alexandrov, I. and P. Lucht. Physics of Sprinting. American J. Physics 49, 1977.
- Pritchard, W.G. Mathematical Models of Running, SIAM Review 35:359-379, Sep 1992.
- Thompson, W.J. Computing in Applied Science. New Jersey:Wiley, 1994, pp.107-109.
- Dunbar, S. The ODE of World Class Sprints. CODEE Newsletter Spring 1994, pp.7-9. On-line at http://www.codee.org/library/newsletters/Spring%201994. Retrieved on: 9 Jan, 2013.
- Lee, J. (August 22, 2008) Usain Bolt 100m 10 meter Splits and Speed Endurance SpeedEndurance.com. Retrieved on: 9 Jan 2013.
- These values for \(a_0\) and \(\tau\) were derived using some split data for Bolt's run. If we start with the two parameter velocity function \(v(t) = a(1 - e^{-b t})\) and integrate, we can find the function \(d(t) = \frac a b(-1 + e^{-bt} + bt)\) for Bolt's distance traveled. Then, using data from [6] for Usain Bolt's splits in the race, we can fit this to obtain a best estimate for the parameters \(a\) and \(b\). This gives the differential equation \(v' = 8.730 - 0.721 v\). In a previous, similar, calculation the equation was found to be \(v' = 9.253 - 0.777 v\).
