Math 215 Examples

Key Concepts

Curl of a Vector Field

The curl is sometimes denoted \(\nabla\times \vec r\), which is sometimes useful for remembering the definition of the curl, as \[\begin{aligned} \nabla\times\vec r &= \left \langle \frac{\partial}{\partial x}, \frac{\partial}{\partial x}, \frac{\partial}{\partial x} \right\rangle \times \langle f, g, h \rangle\\ &= \left \langle \frac{\partial h}{\partial y} - \frac{\partial g}{\partial z}, \frac{\partial f}{\partial z} - \frac{\partial h}{\partial x}, \frac{\partial g}{\partial x} - \frac{\partial f}{\partial y} \right\rangle. \end{aligned}\]

Intuitively, the curl measures the infinitesimal rotation around a point. This is difficult to visualize in three dimensions, but we will soon see this very concretely in two dimensions.

Curl in Two Dimensions

Suppose we have a two-dimensional vector field \(\vec r(x,y) = \langle f(x,y), g(x,y)\rangle\). We can imagine this as a three-dimensional vector field by adding a \(z\)-coordinate of \(0\): \(\vec r(x,y,z) = \langle f(x,y), g(x,y), 0 \rangle \). Then we have \[ \nabla\times \vec r = \langle 0, 0, g_x - f_y \rangle. \] Since the \(x\)- and \(y\)-coordinates are both \(0\), the curl of a two-dimensional vector field always points in the \(z\)-direction. We can think of it as a scalar, then, measuring how much the vector field rotates around a point.

Suppose we have a two-dimensional vector field representing the flow of water on the surface of a lake. If we place paddle wheels at various points on the lake, then the flow of water will cause the wheels to rotate:

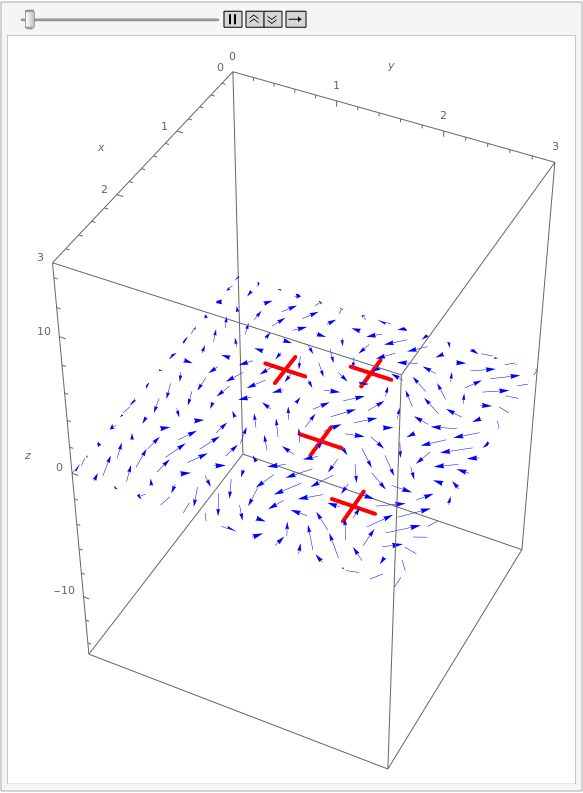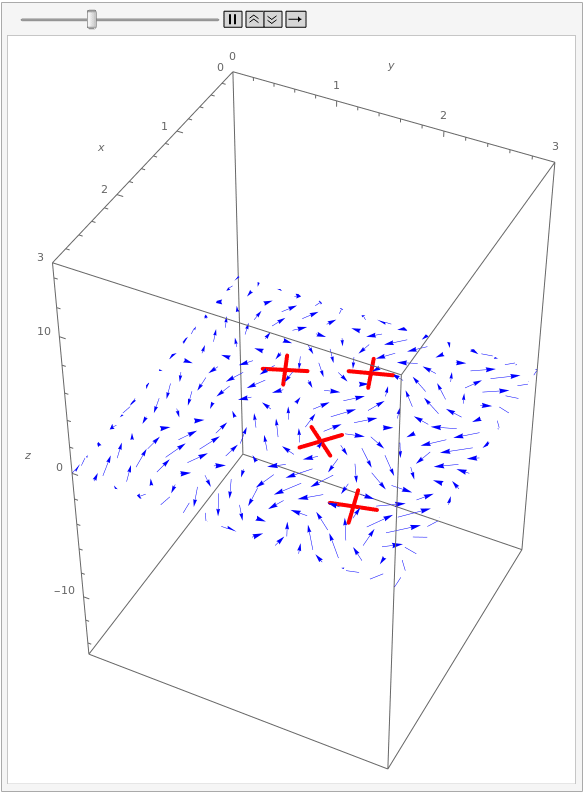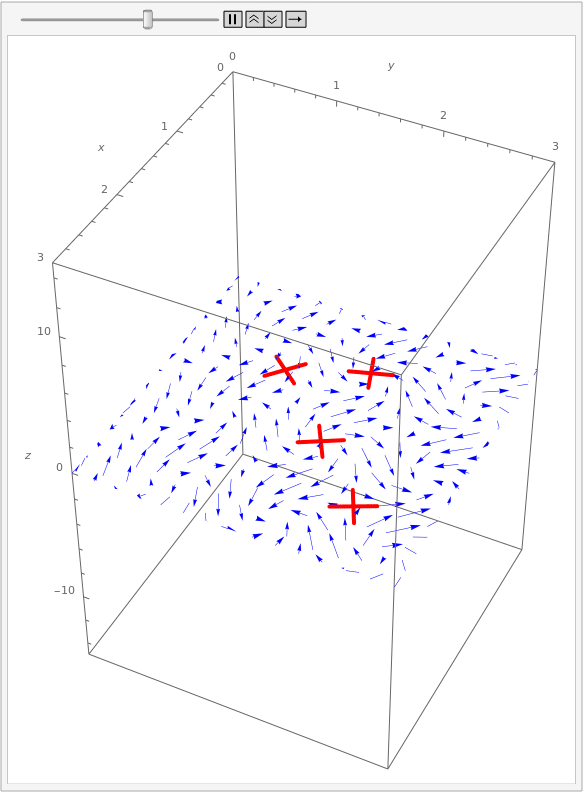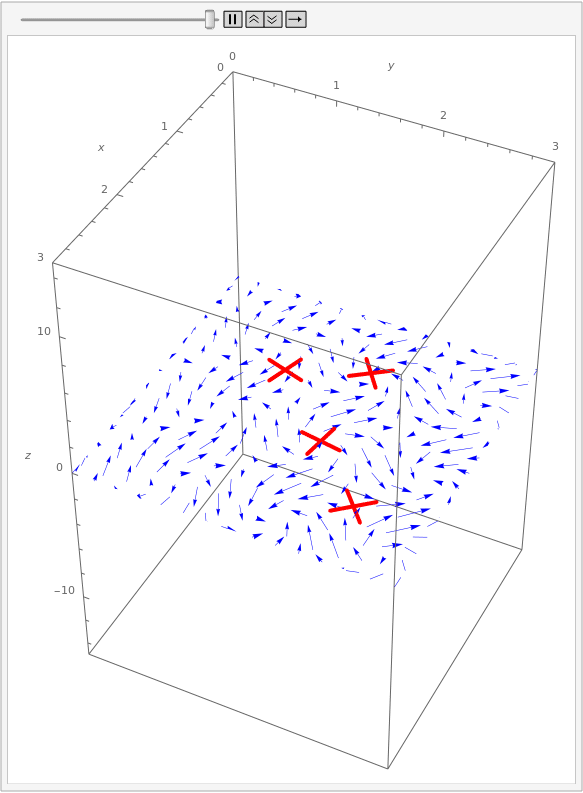
Notice that there are two wheels rotating quite quickly. Around one of them, the water flows consistently clockwise, causing the paddle to rotate clockwise. Around the other, the water flows consistently counter-clockwise, causing the paddle to rotate accordingly. In contrast, the wheel on the left is rotating very slowly. Looking at the vectors near it, we see that some of them are trying to push the wheel clockwise, and some are trying to push counter-clockwise. The net result is that the wheel rotates very little.

Let's now look at the curl of this vector field. Shown below is the same animation, but with the curl drawn as a surface over the vector field. Additionally, green arrows at each paddle show the curl at those points.

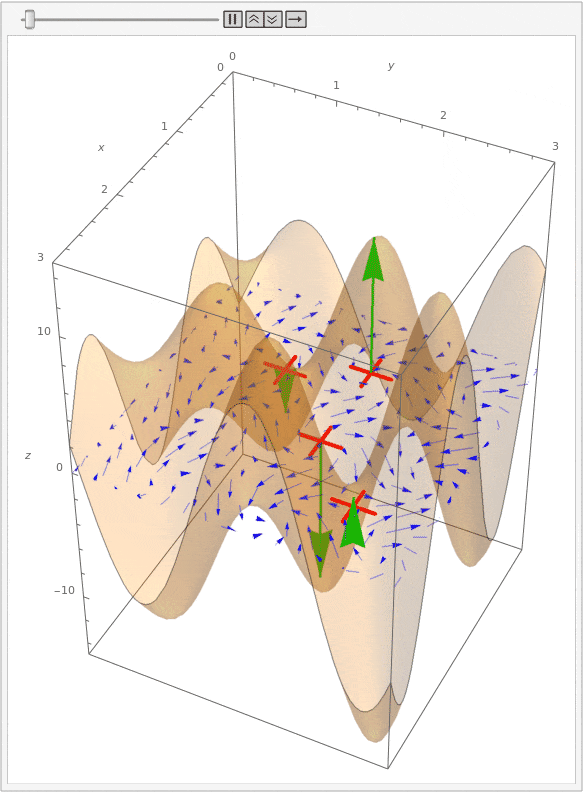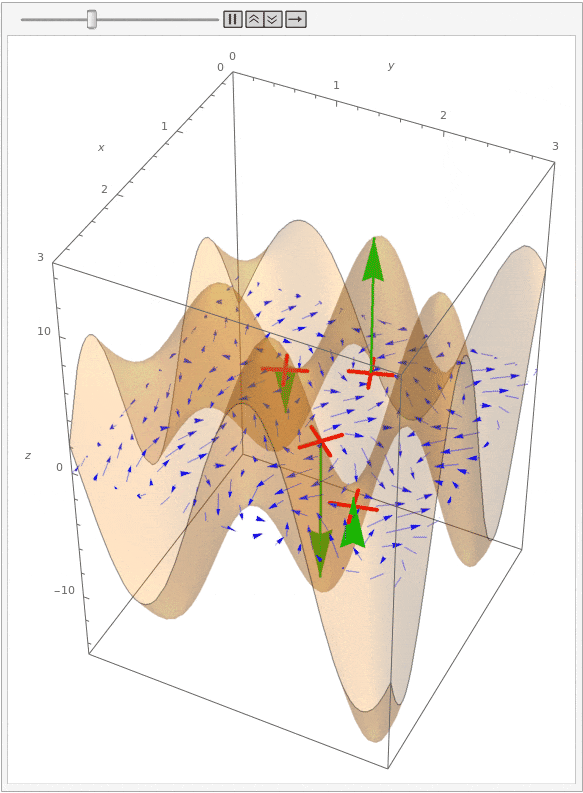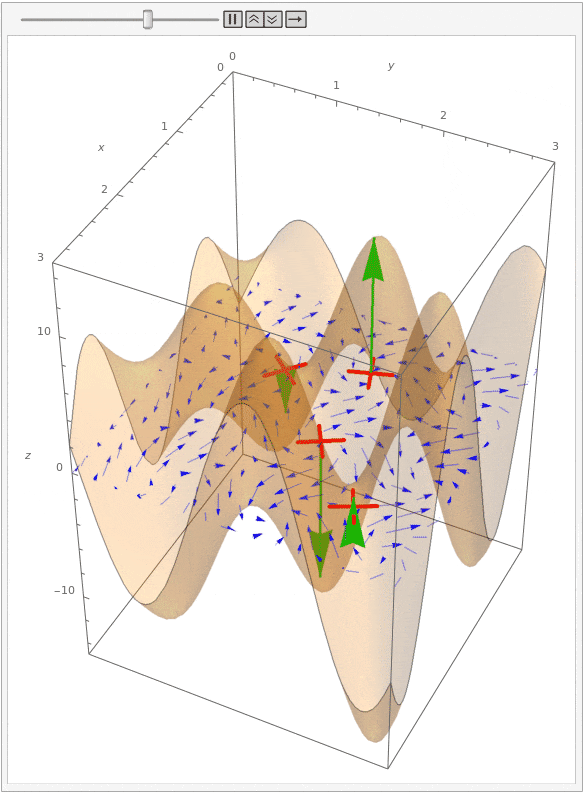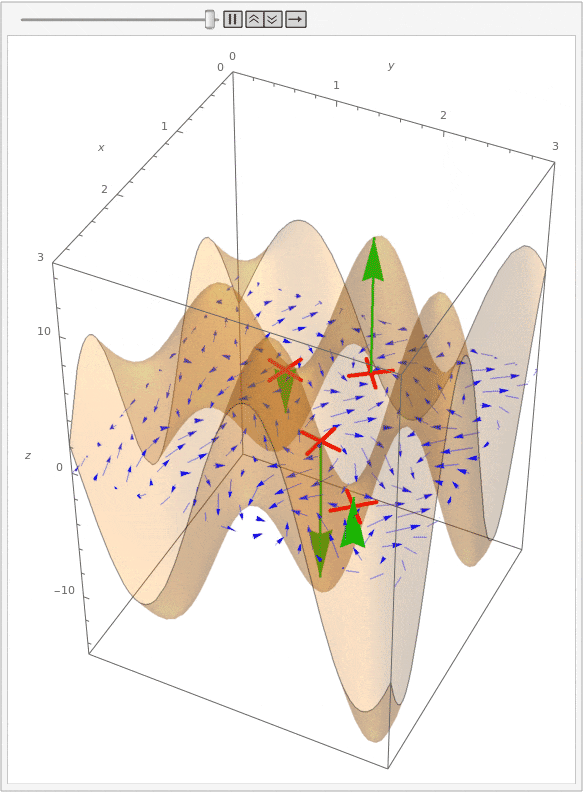
Notice that we can tell how quickly a paddle wheel rotates by the magnitude of the curl, and we can tell whether each wheel rotates clockwise or counter-clockwise by the direction of the curl. This direction follows a "right-hand rule": if you curl your right hand so that your index finger through pinkie follows the flow of water around a point, then your thumb will point in the direction of the curl vector. (This also works in three dimensions, though it is harder to see the rotation.)

Illustrated Example

Worked Solution

We compute \[\begin{aligned} \nabla\times \vec r &= \left\langle 0, 0, \frac{\partial}{\partial x}(\sin(x-y)) - \frac{\partial}{\partial y}{\cos(x+y)} \right\rangle \\ &= \langle 0, 0, \cos(x-y) + \sin(x+y) \rangle. \end{aligned}\] Since the curl points entirely in the \(z\)-direction, the magnitude is just the absolute value of \[ f(x,y) = \cos(x-y) + \sin(x+y), \] so we look for local extrema of this function on the given region.

To find local extrema, we take the gradient \[ \nabla f(x,y) = \langle -\sin(x-y)+\cos(x+y), \sin(x-y)+\cos(x+y) \rangle. \] To be a local extremum, we need both components to be zero; i.e., we need \( -\sin(x-y) + \cos(x+y) = 0\) and \(\sin(x-y) + \cos(x+y) = 0\). This is only possible if (\sin(x-y) = \cos(x+y) = 0\), and so we see that \(x-y = 0 + k\pi\) for some integer \(k\) and \(x+y = \pi/2 + j\pi\) for some integer \(j\). The only possible solution in our domain is \(x = y = \pi/4\), at which point the curl is \(\cos(0) + \sin(\pi/2) = 2\). Since this is the maximum possible value of \(\cos(x-y)+\sin(x+y)\) (since cosine and sine can be at most \(1\) each), this must be a local (and in fact global) maximum for the curl.

We conclude, then, that the maximum magnitude of the curl is \(2\) at the point \((\pi/4, \pi/4)\).

Visualizing the Example

The image below shows the vector field with the magnitude of the curl drawn as a surface above it:

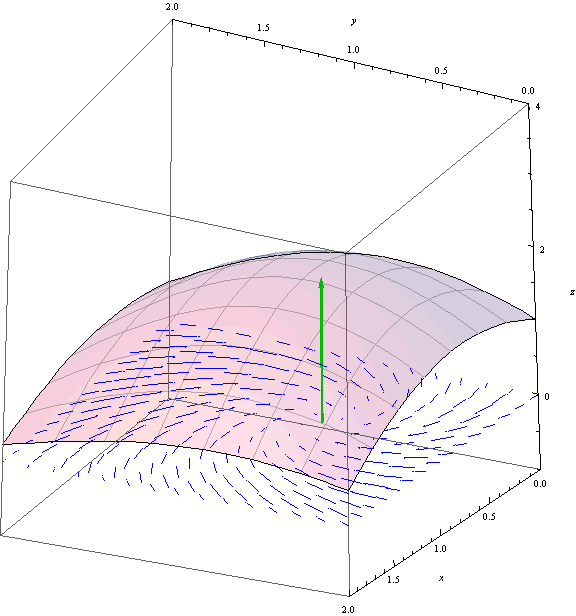
The green arrow is the curl at \((\pi/4, \pi/4)\). Notice that the vector field looks very much like a whirlpool centered at the green arrow. Intuitively, then, we would guess that the rotation of the flow is greatest at the center of this whirlpool, and indeed, that is precisely what we just computed.

Further Questions

1. In the example, why must both \(\sin(x-y)\) and \(\cos(x+y)\) be zero to have a critical point of \(f(x,y)\)?
2. What is the value of \(\vec r(x,y)\) at the point found in the example? Can you modify \(\vec r(x,y)\) so that the maximum curl still occurs at \((\pi/4, \pi/4)\), but so that \(\vec r(x,y)\) has a different value at this point?
3. Can you come up with a formula for a two-dimensional vector field \(\vec r(xy)\) with constant nonzero curl at every point?
4. Let \(f(x,y,z)\) be a (scalar-valued) function, and assume that \(f(x,y,z)\) is infinitely differentiable. Its gradient \(\nabla f(x,y,z)\) is a vector field. What is the curl of the gradient? Can you come to the same conclusion with an assumption weaker than infinite differentiability?

Using the Mathematica Demo

All graphics on this page were generated by the Mathematica notebook 16_5_Curl.nb.

This notebook generates images and animations like those on this page for any two-dimensional vector field.

As an exercise, use the notebook to animate a paddle wheel at the point \((\pi/4, \pi/4)\) in the example, and provide a graphical demonstration of your answers to Questions 2 and 3.

Think about what sorts of two-dimensional vector fields might have large curls, and try to guess some formulas for them. Then use the notebook to see graphically whether your intuition about the curl was correct.