Math 215 Examples

Key Concepts

Polar Rectangles

A polar rectangle is a region in the \(xy\)-plane defined by the inequalities \(a \le r \le b\) and \(\alpha\le\theta\le\beta\) in polar coordinates. For example, the unit disk can be concisely described as the polar rectangle \(0\le r\le 1\), \(0\le\theta\le 2\pi\).

The area of a polar rectangle is \(\frac{1}{2}(\beta-\alpha)(b^2-a^2)\), as this is the difference in area between the sectors of a radius \(b\) and a radius \(a\) circle for \(\alpha\le\theta\le\beta\).

In particular, if we have a polar rectangle of radial "width" \(\Delta r\) and angular "width" \(\Delta \theta\) centered around \((r,\theta)\), then \(\beta-\alpha=\Delta\theta\) and \(\frac{1}{2}(b^2-a^2)=\frac{1}{2}(b+a)(b-a) = r\Delta r\), so the area of this polar rectangle is \(r \Delta r\Delta\theta\).

Integrating in Polar Coordinates

Recall that, to estimate \(\iint\limits_R f(x,y)\,dA\) over an ordinary rectangle \(R\), we formed the Riemann sum \[\iint\limits_R f(x,y)\,dA \approx \sum_{i=1}^m\sum_{j=1}^n f(x_i,y_j)\Delta A = \sum_{i=1}^m\sum_{j=1}^n f(x_i,y_i)\Delta x\Delta y\] where each \((x_i,y_j)\) is a sample point in the \(ij\)th subrectangle. Taking the limit as the number of subrectangles goes to infinity is, in fact, our definition of \(\iint\limits_R f(x,y)\,dA\).

What if instead we want to integrate \(f(x,y)\) over a polar rectangle \(R\)? We can write \(f(x,y)\) in polar coordinates as \(f(r\cos\theta, r\sin\theta)\) by using the relations \(x=r\cos\theta\), \(y=r\sin\theta\). Now if we subdivide \(R\) into polar subrectangles, we have \[\iint\limits_R f(x,y)\,dA \approx \sum_{i=1}^m\sum_{j=1}^n f(r_i\cos\theta_j, r_i\sin\theta_j)\Delta A\] where each \((r_i,\theta_j)\) is a sample point in the \(ij\)th polar subrectangle.

For example, a Riemann sum over a polar rectangle with \(4\) radial subdivisions and \(3\) angular subdivisions might look graphically like

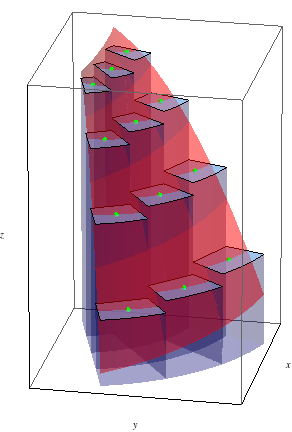
If we pick the sample points in the Riemann sum to be the centers of the polar subrectangles, then as just discussed, we can write \(\Delta A = r_i\Delta r\Delta\theta\), and our Riemann sum becomes \[\iint\limits_R f(x,y)\,dA \approx \sum_{i=1}^m\sum_{j=1}^n f(r_i\cos\theta_j, r_i\sin\theta_j) r_i\Delta r\Delta\theta\] (notice the \(r_i\) arising from \(\Delta A\) on the right hand side!).

Taking the limit as \(m\) and \(n\) go to infinity turns the right hand side into an iterated integral:

Illustrated Example

Worked Solution

The region \(R\) is the polar rectangle \(0\le r\le 1\), \(\pi/2\le\theta\le\pi\). Using \(x=r\cos\theta\) and \(y=r\sin\theta\), we write the integrand in polar coordinates as \[\begin{aligned} x^2-3x+y^2 &= (r\cos\theta)^2-3r\cos\theta+(r\sin\theta)^2 \\ &= r^2(\cos^2\theta+\sin^2\theta)-3r\cos\theta \\ &= r^2 - 3r\cos\theta. \end{aligned}\]

Remembering to include the extra factor of \(r\) when converting to polar coordinates, the desired integral is \[\begin{aligned} \iint\limits_R (x^2-3x+y^2)\, dA &= \int_{\pi/2}^\pi\int_0^1 (r^2-3r\cos\theta)\,r\,dr\,d\theta \\ &= \int_{\pi/2}^\pi\int_0^1 (r^3-3r^2\cos\theta)\,dr\,d\theta \\ &= \int_{\pi/2}^\pi\left(\left(\frac{1}{4}r^4-r^3\cos\theta\right)\Bigg|_0^1\right)\, d\theta \\ &= \int_{\pi/2}^\pi\left(\frac{1}{4}-\cos\theta\right)\,d\theta \\ &= \left(\frac{1}{4}\theta-\sin\theta\right)\Bigg|_{\pi/2}^\pi \\ &= \left(\frac{\pi}{4}+0\right)-\left(\frac{\pi}{8}-1\right) \\ &= \frac{\pi}{8}+1. \end{aligned}\]

Visualizing the Example

The following animation shows the polar Riemann sums approximating this double integral as the number of subdivisions increases.

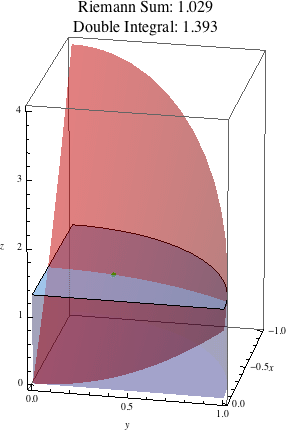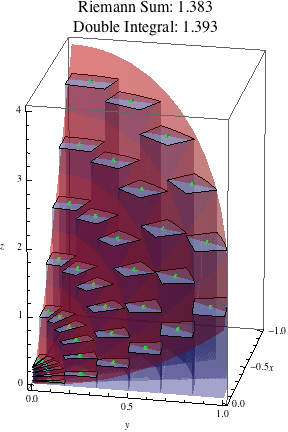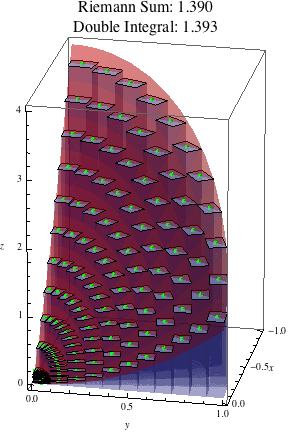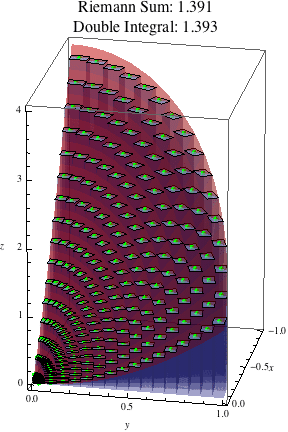
Notice that the polar rectangles closer to the origin are much narrower looking than the ones further out, so if we had two boxes in a polar Riemann sum with the same height, the one closer to the origin would contribute less to the result than the one further out. This is not true in the ordinary, non-polar Riemann sums we've looked at; in these sums, all the subrectangles have the same area \(\Delta A = \Delta x \Delta y\), so two boxes with the same height have the same volume and hence always contribute the same amount to the Riemann sum. However, in polar Riemann sums, the area of a polar subrectangle is \(\Delta A = r\Delta r\Delta\theta\), which depends also on \(r\), the distance from the origin. Thus polar subrectangles closer to the origin (with small \(r\)) contribute less to the result than polar subrectangles further from the origin (with bigger \(r\)). We see this graphically in the narrow rectangles near the origin, and symbolically in the extra factor of \(r\) that shows up when writing the double integral as an iterated integral in polar coordinates.

Further Questions

1. Work this example again using the other order of integrals, integrating first with respect to \(\theta\) then \(r\).
2. How would our answer change if our region of integration were instead the sector of the unit disk in the first quadrant? What about the third quadrant? Fourth quadrant? Try to answer these questions without redoing the whole calculation; instead, think about which parts of the calculation would change, and how.
3. Based on your answers to Question 2, what would we get if we integrated \(x^2-3x+y^2\) over the entire unit disk?
4. In the box on Double Integrals in Polar Coordinates, we defined the angular range as \(\alpha\le\theta\le\beta\), with \(0\le \beta-\alpha\le 2\pi\). What could go wrong with our polar rectangles if we allow \(\beta-\alpha > 2\pi\)?
5. In the box on Double Integrals in Polar Coordinates, we defined the radial range as \(0\le a\le r\le b\). What could go wrong with our polar rectangles if we allow \(a < 0\)?

Using the Mathematica Demo

All graphics on this page were generated by the Mathematica notebook 15_4DoubleIntegralsInPolarCoordinates.nb.

This notebook generates images and animations like those on this page of polar Riemann sums for any integrand \(f(r,\theta)\) and any polar rectangle.

As an exercise, use the notebook to provide clear graphical answers to Questions 2 and 3 above.

Then, can you come up with an integrand \(f(r,\theta)\) and bounds so that the notebook produces Riemann sums approximating the area of the unit circle, or the volume of the unit sphere? What about a cone of radius 1 and height 1?