Key Concepts
Statement of Fubini's Theorem
This section is all about computing double integrals by means of Fubini's Theorem:
Intuition behind Fubini's Theorem
Recall that we can think of the double integral \(\iint_R f(x,y)\, dA\) appearing on the left-hand side of Fubini's theorem as the signed volume between \(f(x,y)\) and the \(xy\)-plane:
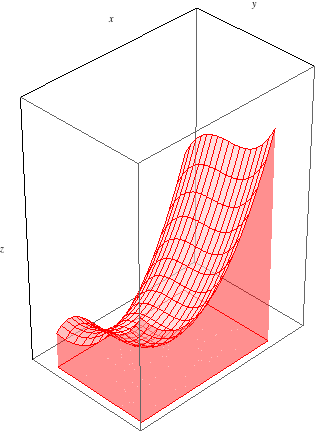
Let's first consider \(\int_a^b\int_c^d f(x,y)\, dy\, dx\), which, according to Fubini's Theorem, should equal the same signed volume. To evaluate this iterated integral, we work from the inside out. First, we evaluate the inner integral \(\int_c^d f(x,y)\, dy\). Since this integral is with respect to \(y\), we treat \(x\) as constant throughout, so our result will depend on \(x\). Let's call it \(g(x) = \int_c^d f(x,y)\, dy\). What is, say, \(g(x_0)\), for some \(a\le x_0\le b\)? \(g(x_0) = \int_c^d f(x_0,y)\, dy\) gives the slice of area at \(x=x_0\) between the function and the \(xy\)-plane:
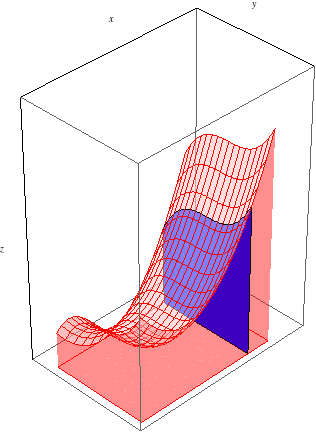
As we integrate from \(x=a\) to \(x=b\), these slices of area sweep out the entire volume between \(f(x,y)\) and the \(xy\)-plane:
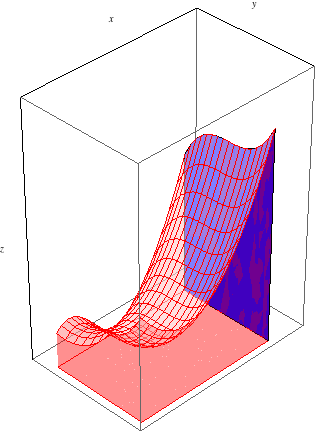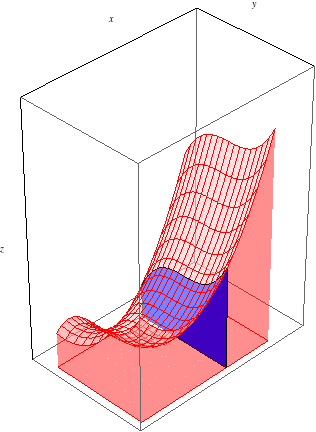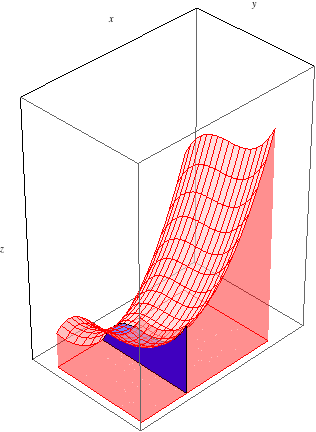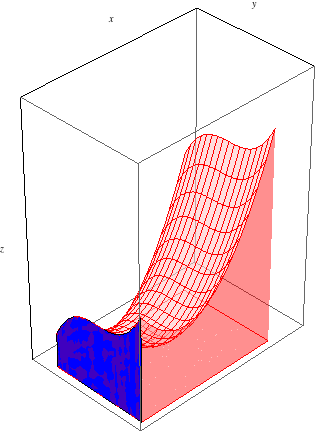
We see, then, that this iterated integral should indeed equal the signed volume between \(f(x,y)\) and the \(xy\)-plane, just as Fubini's Theorem states.
Fubini's Theorem also says that we can do the integrals in the other order, so \(\int_c^d\int_a^b f(x,y)\, dx\, dy\) should also yield the same signed volume. The inner integral now corresponds to the area of a slice at a fixed \(y\) value, and the outer integral sweeps out the volume as we range from \(y=c\) to \(y=d\):
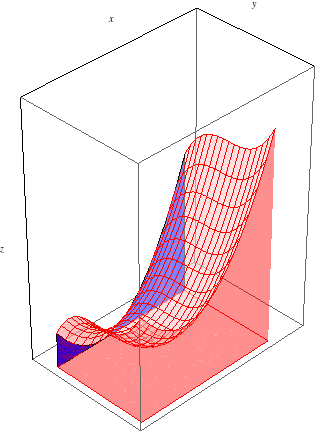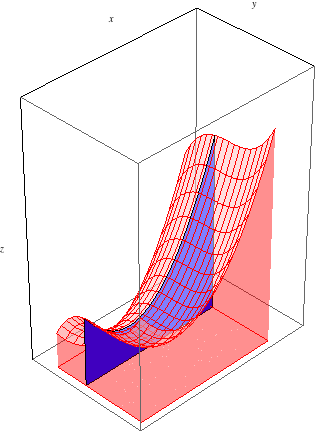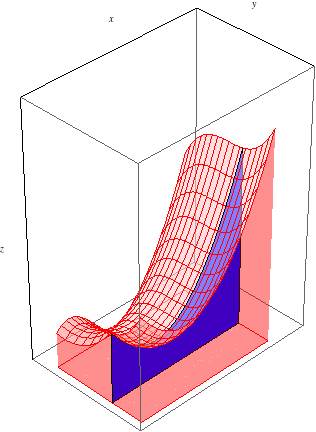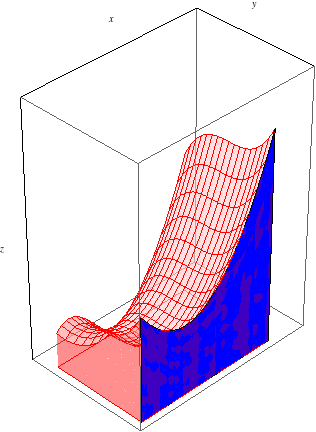
Illustrated Example
Worked Solution
We use Fubini's Theorem to write \[\iint\limits_R (x^3+y^2+1)\, dA = \int_{-1}^1\int_{-2}^1 (x^3+y^2+1)\, dy\, dx.\]
We evaluate the inner integral as a standard single-variable integral with respect to \(y\), treating \(x\) as constant: \[\begin{aligned} \int_{-2}^1 (x^3+y^2+1)\, dy &= (x^3y+y^3/3+y)\Big|_{y=-2}^{y=1} \\ &= (x^3+4/3)-(-2x^3-14/3) \\ &= 3x^3+6. \end{aligned}\]
Hence \[\begin{aligned} \int_{-1}^1\int_{-2}^1 (x^3+y^2+1)\, dy\, dx &= \int_{-1}^1 (3x^3+6)\, dx \\ &= (3x^4/4 + 6x)\Big|_{-1}^1 \\ &= (3/4 + 6)-(3/4-6) \\ &= 12, \end{aligned}\] so we conclude that \(\iint\limits_R (x^3+y^2+1)\, dA = 12\).
Visualizing the Example
As we did above in Key Concepts, define \(g(x)\) to be the inner integral \[g(x) = \int_{-2}^1 (x^3+y^2+1)\, dy.\] For any \(x_0\), we think of \(g(x_0)\) as giving us the area of the slice at \(x=x_0\). For example, \[g(-1/2) = \int_{-2}^1 (y^2+7/8)\, dy\] gives the area of the slice at \(x=-1/2\):
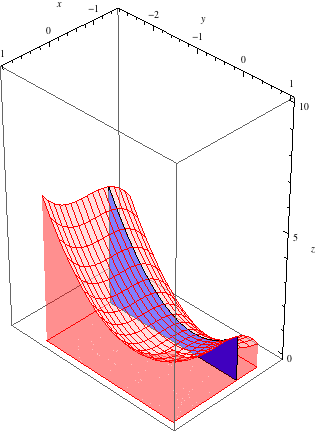
Notice that the top of the slice looks like a parabola; indeed, it is the parabola \(z=f(-1/2,y)=y^2+y/8\), the integrand appearing in \(g(-1/2)\).
Let's keep track of the area of each slice as we sweep from \(x=-1\) to \(x=1\). In the animation below, the red curve behind the surface shows the area of the slice as a function of \(x\). In other words, the red curve is the graph of the (single-variable) function \(z = g(x)\).
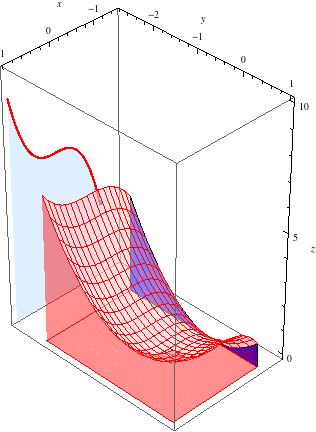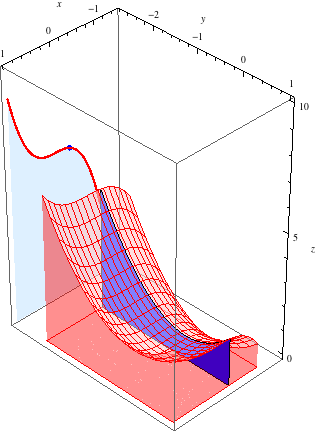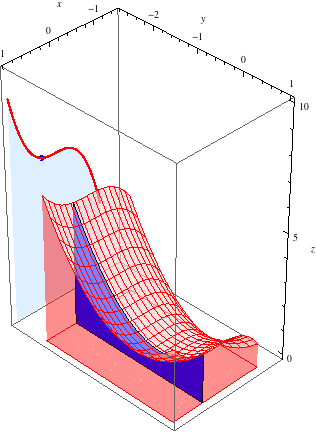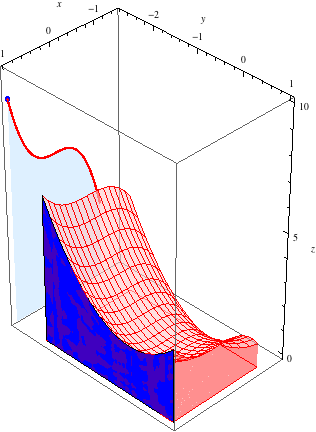
This curve looks like the graph of a cubic polynomial, and indeed, it is the graph of \[z = g(x) = \int_{-2}^1 (x^3+y^2+1)\, dy = 3x^3+6.\]
Further Questions
- Work this example again using the other order of integrals provided by Fubini's Theorem, \(\int_{-2}^1\int_{-1}^1 (x^3+y^2+1)\, dx\, dy\).
- With this order, our slices are now at fixed \(y\)-values. What does the top of each slice look like? Think about your answer graphically as well as symbolically.
- Again with this order of integration, if we imagine plotting the area of each slice as a function of \(y\), what kind of curve do we get? Think about your answer graphically as well as symbolically.
Using the Mathematica Demo
All graphics on this page were generated by the Mathematica notebook 15_2IteratedIntegrals.nb.
This notebook generates images and animations like those on this page for any integrand \(f(x,y)\) and any bounds. Additionally, you can toggle on and off various elements in the images, and you can choose whether to take slices as fixed \(x\)-values or at fixed \(y\)-values by choosing which to consider as the inner integral.
As an exercise, use the notebook to provide clear graphical answers to Questions 2 and 3 above. Can you come up with an integrand \(f(x,y)\) so that the answers to Questions 2 and 3 are linear functions? Sinusoidal? Exponential? Can you find an integrand so that slices in one direction are sinusoidal, and slices in another are linear?