Math 215 Examples

Key Concepts

Partial Derivatives

Recall that, in single variable calculus, the derivative of a function \(f(x)\) is defined as \[ \frac{d}{dx}f(x) = \lim_{h\to 0}\frac{f(x+h)-f(x)}{h}. \] Alternatively, we often write \(f'(x)\) for the derivative.

Now suppose \(f(x,y)\) is a function of two variables. If we treat \(y\) as a constant, we can think of \(f(x,y)\) as a function single-variable function of \(x\) and take its derivative. Likewise, we could treat \(x\) as a constant and take the derivative with respect to \(y\). This leads to the following definition:

Alternatively, we often write \(f_x(x,y)\) for the partial derivative with respect to \(x\) and \(f_y(x,y)\) for the partial derivative with respect to \(y\).

Similarly, if we had a function of three or more variables, we can likewise define partial derivatives with respect to each of these variables as well.

Partial Derivatives As Slopes

What do the partial derivatives mean graphically? Let's suppose we want to consider the partial derivatives of a function \(f(x,y)\) at a point \((x_0,y_0)\). Consider as well the single-variable functions \(g(x) = f(x,y_0)\) and \(h(y) = h(x_0,y)\). The curves given by \(C_1=(x,y_0,g(x))\) and \(C_2=(x_0,y,h(y))\) lie on the surface \(z=f(x,y)\) and intersect at the point \((x_0,y_0,f(x_0,y_0))\). The partial derivatives, then, equal the derivatives of \(g(x)\) and \(h(x)\): \[\begin{aligned} f_x(x_0,y_0) &= g'(x_0) \\ f_y(x_0,y_0) &= h'(y_0). \end{aligned}\] Hence \(f_x(x_0,y_0)\) gives the slope of the curve through the surface at \(y=y_0\), and \(f_y(x_0,y_0)\) gives the slope of the curve through the surface at \(x=x_0)\).

Tangent Vectors and Tangent Planes

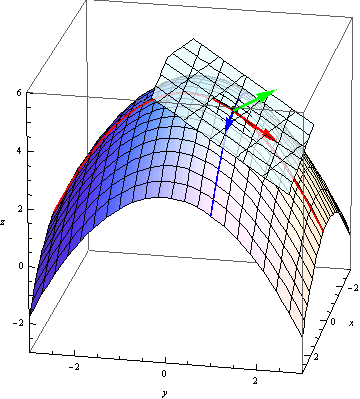
We can visualize this by imagining tangent vectors to the surface. Notice that the vector \(\vec u=\langle 1, 0, f_x(x_0,y_0)\rangle\) is tangent to the curve \(C_1\) at the point \((x_0,y_0)\), and the vector \(\vec v=\langle 0, 1, f_y(x_0,y_0)\rangle\) is tangent to the curve \(C_2\) at the point \((x_0,y_0)\):

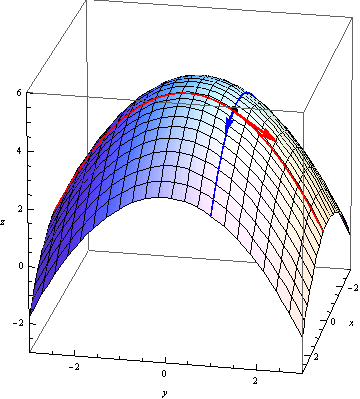
Now that we have two vectors tangent to the surface, we can use them to find a normal vector to the tangent plane. The cross product of these two tangent vectors is \[\vec u\times\vec v = \langle -f_x(x_0,y_0),-f_y(x_0,y_0),1\rangle\] and so we find as an equation of the tangent plane \[\ -f_x(x_0,y_0) (x-x_0) - f_x(x_0,y_0) (y-y_0) + (z-f(x_0,y_0)) = 0. \]

Illustrated Example

Worked Solution

Let \(f(x,y) = ax^2+by^2+c\). For the two surfaces to intersect at \((1,1,1)\), we need \(f(1,1)=1\), or \(a+b+c=1\).

To be tangent, we need the two surfaces to have parallel normal vectors at \((1,1,1)\). Since the radius of a sphere is perpendicular to its surface, we have that \(\langle 1, 1, 1\rangle\) itself is normal to the sphere. To compute the normal to the surface, we take partial derivatives: \[\begin{aligned} f_x(x,y) &= 2ax \\ f_y(x,y) &= 2by \end{aligned}\] and hence \(f_x(1,1) = 2a\) and \(f_y(1,1)=2b\). The vectors \(\langle 1, 0, 2a\rangle\) and \(\langle 0, 1, 2b\rangle\) are therefore both tangent to the surface \(z=f(x,y)\). Their cross product \(\langle -2a, -2b, 1\rangle\) is therefore normal to the surface \(z=f(x,y)\).

For this to be parallel to the normal to the sphere \(\langle 1, 1, 1\rangle\), we need \[\langle -2a, -2b, 1 \rangle = \lambda \langle 1, 1, 1 \rangle\] for some constant multiple (\lambda\). By considering the \(z\)-components, we see that \(\lambda\) must be \(1\), and then it follows from the other components that \(-2a=1\) and \(-2b=1\). Hence \(a=-\frac{1}{2}\) and \(b=-\frac{1}{2}\).

Combining this with our first observation that \(a+b+c=1\), we see that \(-1+c=1\) or \(c=2\). Hence we conclude that \(a=-\frac{1}{2}\), \(b=-\frac{1}{2}\), and \(c=2\) are the desired values, and so \( z = 2 - \frac{1}{2}x^2 - \frac{1}{2}y^2\) is tangent to \(x^2+y^2+z^2=3\) at the point \((1,1,1)\).

Visualizing the Example

Once we have found the equation \(z = 2-\frac{1}{2}x^2 - \frac{1}{2}y^2\), it is graphically clear that this is tangent to the sphere \(x^2+y^2+z^2=1\) at \((1,1,1)\):

We see that, in fact, the sphere fits inside the downward-facing paraboloid so that they just touch at \((1,1,1)\), with the same tangent vectors and normal vector.

Further Questions

1. Suppose instead we wanted to find \(a\), \(b\), and \(c\) so that the paraboloid was perpendicular to the sphere at the point \((1,1,1)\). How does the calculation change? Is there a unique solution? Find at least one solution.
2. Suppose we had two graphs of functions of three variables, \(w=f(x,y,z)\) and \(w=g(x,y,z)\). What must be true if these two graphs are tangent at the point \((x_0,y_0,z_0)\)?
3. Suppose we \(f(x,y,z)\) is fixed, but \(g(x,y,z)\) depends on three parameters. Do you expect us to be able to solve for values of the parameters such that the two graphs are tangent at the point \((x_0,y_0,z_0)\)? What if there were four parameters instead? Five?

Using the Mathematica Demo

All graphics on this page were generated by the Mathematica notebook 14_3_4PartialDerivativeAndTangentPlanes.nb.

This notebook generates images like those on this page for any function and any point.

As an exercise, use the notebook to provide a visual demonstration illustrating your answer to Question 1.

Investigate other surfaces \(z=f(x,y)\) and their partial derivatives. What does a surface look like at a point where one or both of its partial derivatives are zero? Do all points where the partials are zero exhibit the same local behavior? Find as many different-looking examples as you can of what a surface can look like when near a point with one or both partial derivatives equal to zero. (Then come back and think about your examples once you've covered Section 14.6 and 14.7.)