Key Concepts
Tangent Vectors
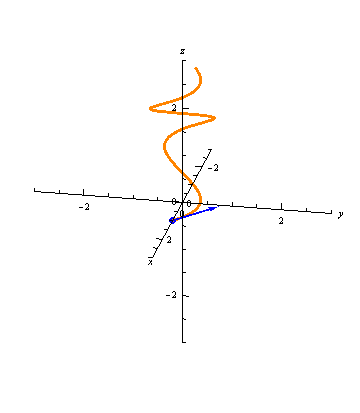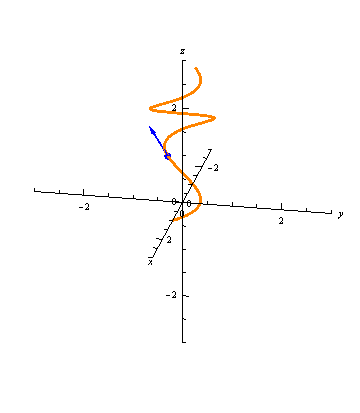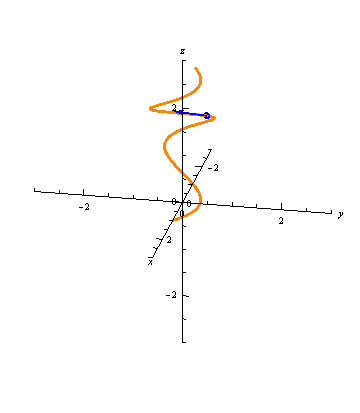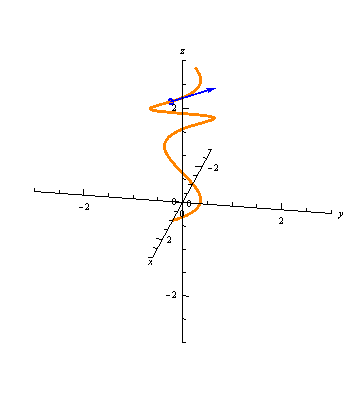
Let \(\vec r(t) = \langle x(t), y(t), z(t) \rangle\) be a curve. Then the vector-valued function \(\vec r'(t) = \langle x'(t), y'(t), z'(t) \rangle\) gives a tangent vector to the curve at any time \(t\). The unit tangent vector is \[\vec T(t) = \frac{\vec r'(t)}{||\vec r'(t)||}.\]
Note that the unit tangent vector is just the derivative \(\vec r'(t)\) normalized. While \(\vec r'(t)\) depends on the parameterization, \(\vec T(t)\) does not (as long as both parameterizations move through the curve in the same direction). If \(||\vec r'(t)||=1\) for all \(t\) (i.e., \(\vec r'(t) = \vec T(t)\)), then we say that \(r(t)\) is the unit speed parameterization of the curve.
The unit tangent vectors are graphically intuitive, as we are used to thinking about tangent lines of curves:
Normal Vectors
At any time \(t\), the vector-valued function \(\vec T'(t)\) gives a vector orthogonal to the unit tangent \(\vec T(t)\). The unit normal vector is \[\vec N(t) = \frac{\vec T(t)}{||\vec T'(t)||}.\]
Note that, for an arbitrary vector-valued function \(\vec s(t)\), it is not generally true that \(\vec s'(t)\) and \(\vec s(t)\) are normal to each other. However, if \(\vec s(t)\) is a unit speed parameterization (i.e., if \(||\vec s(t)||=1\) for all \(t\)), then \(\vec s'(t)\) and \(\vec s(t)\) are indeed normal. This is the situation in the definition of normal vectors: since \(||\vec T(t)||=1\), \(\vec T'(t)\) and \(\vec T(t)\) are orthogonal. Note, though, that just because \(\vec T(t)\) is always a unit vector, \(\vec T'(t)\) is not necessarily a unit vector. Hence to get the unit tangent \(\vec N(t)\), we must normalize \(\vec T'(t)\).
Graphically, the normal vector points "inward," as seen in the following animation:
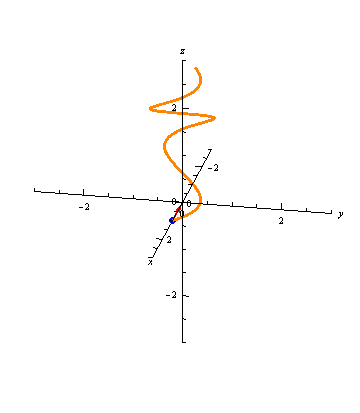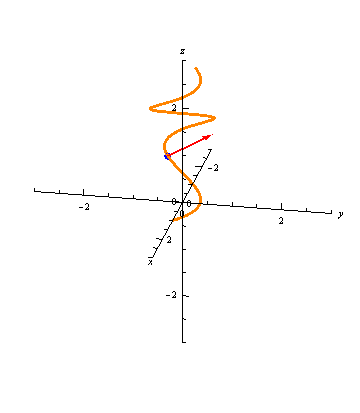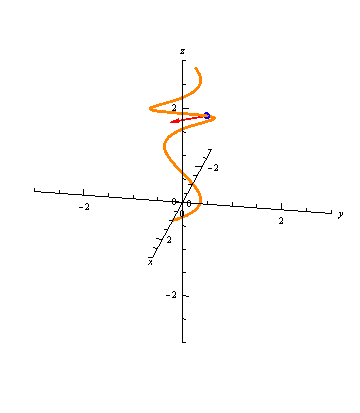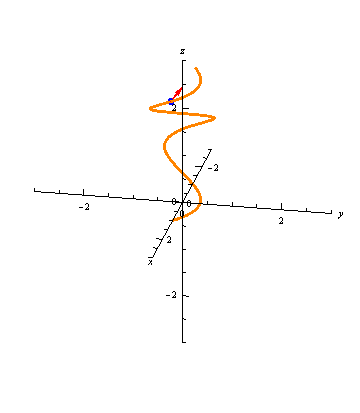
Binormal Vectors
The binormal vector is \[\vec B(t) = \vec T(t)\times \vec N(t).\]
As a cross product, \(\vec B(t)\) is automatically orthogonal to both \(\vec T(t)\) and \(\vec N(t)\). Since \(\vec T(t)\) and \(\vec N(t)\) are orthogonal and are both unit vectors, \(\vec B(t)\) is also a unit vector.
Normal Planes
At any point \(t\), the plane through the point \(\vec r(t)\) and normal to the tangent vector \(\vec T(t)\) is called the normal plane to the curve at \(t\). The unit normal vector \(\vec N(t)\) and the binormal vector \(\vec B(t)\) are both orthogonal to \(\vec B(t)\), and hence they both lie in the normal plane:
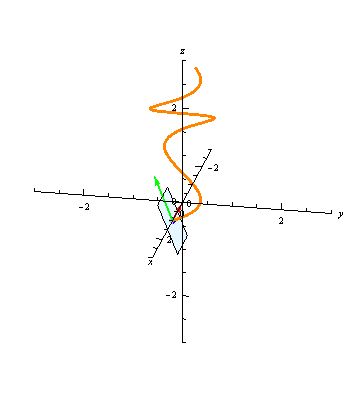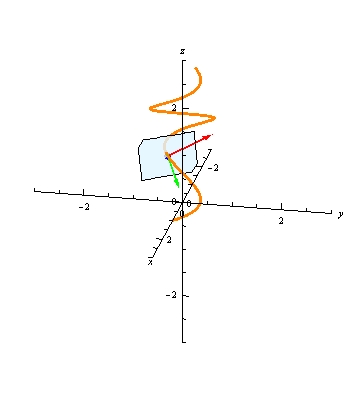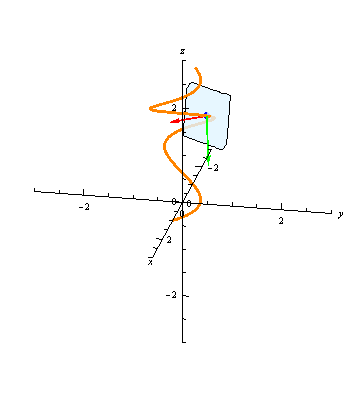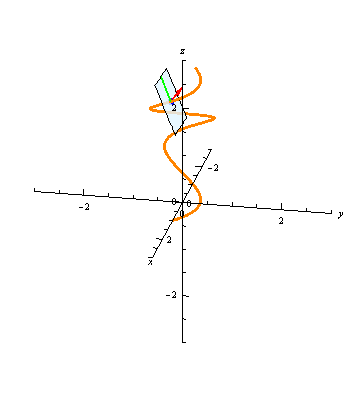
The binormal vector, then, is uniquely determined up to sign as the unit vector lying in the normal plane and orthogonal to the normal vector.
TNB Frames
For any \(t=t_0\), we now have three vectors, \(\vec T(t_0)\), \(\vec N(t_0)\), and \(\vec B(t_0)\), all orthogonal, and all unit vectors. These define an orthonormal basis for the 3-dimensions coordinate system: for any vector \(\vec v\), we can write it as \[ \vec v = (\vec v\cdot \vec T(t_0)) \vec T(t_0) + (\vec v\cdot \vec N(t_0)) \vec N(t_0) + (\vec v\cdot \vec B(t_0)) \vec B(t_0). \] This basis is called the TNB frame of the curve at \(t=t_0\). The animation below shows the TNB frame of a curve at each point.
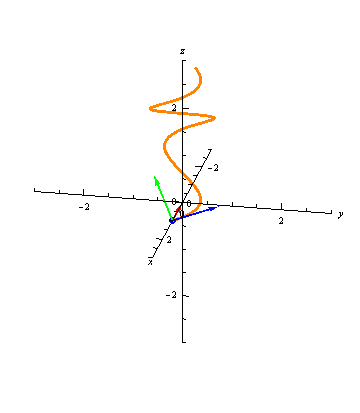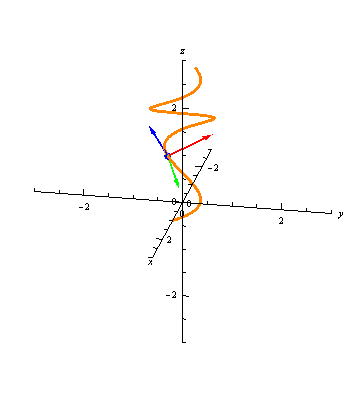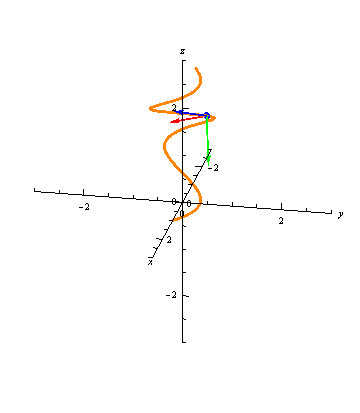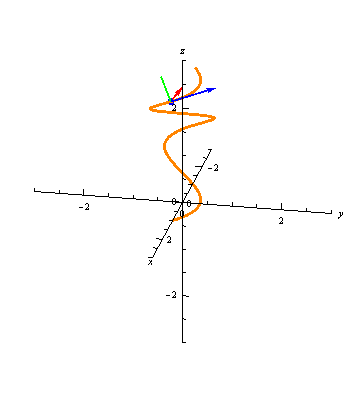
Illustrated Example
Find the unit normal vector and an equation for the normal plane for \(\vec r(t) = \langle t, t^2, t^3 \rangle\) at \(t=2\).
Worked Solution
We start by finding \(\vec r'(t)\): \[ \vec r'(t) = \langle 1, 2t, 3t^2 \rangle. \] The magnitude of this vector is \[ ||\vec r'(t)|| = \sqrt{1^2 + (2t)^2 + (3t^2)^2} = \sqrt{1+4t^2+9t^4}, \] so we have \[ \vec T(t) = \frac{\vec r'(t)}{||\vec r'(t)||} = \left\langle \frac{1}{\sqrt{1+4t^2+9t^4}}, \frac{2t}{\sqrt{1+4t^2+9t^4}}, \frac{3t^2}{\sqrt{1+4t^2+9t^4}} \right\rangle. \] At this point, we could plug in \(t=2\) to find the unit tangent vector at this point. Unfortunately, in order to find the unit normal vector, we need to differentiate \(\vec T(t)\), so we can't plug in \(t=2\) yet. So we proceed with finding \(\vec T'(t)\). Noting that \[ \frac{d}{dt}\left(\sqrt{1+4t^2+9t^4}\right) = \frac{8t+36t^3}{2\sqrt{1+4t^2+9t^4}}, \] we have \[ \vec T'(t) = \left\langle \frac{-\frac{8t+36t^3}{2\sqrt{1+4t^2+9t^4}}}{1+4t^2+9t^4}, \frac{2\sqrt{1+4t^2+9t^4}-2t\frac{8t+36t^3}{2\sqrt{1+4t^2+9t^4}}}{1+4t^2+9t^4}, \frac{6t\sqrt{1+4t^2+9t^4}-3t^2\frac{8t+36t^3}{2\sqrt{1+4t^2+9t^4}}}{1+4t^2+9t^4} \right\rangle \]
Fortunately, we are now done with messy calculations. Even though \(\vec N(t)\) is defined as the unit vector in this direction, we can plug \(t=2\) into \(\vec T'(t)\) and then normalize. So first we plug in \(t=2\) \[\begin{aligned} \vec T'(2) &= \left\langle \frac{-\frac{304}{2\sqrt{161}}}{161}, \frac{2\sqrt{161}-4\frac{304}{2\sqrt{161}}}{161}, \frac{12\sqrt{161}-12\frac{304}{2\sqrt{161}}}{161} \right\rangle \\ &\approx \langle -0.074, -0.14, 0.053 \rangle. \end{aligned}\] This vector has length \(\sqrt{(-0.074)^2+(-0.14)^2+0.053^2}\approx 0.17\), so we have \[ \vec N(2) = \frac{\vec T'(2)}{||\vec T'(2)||} = \frac{1}{0.17}\langle -0.074, -0.14, 0.053 \rangle = \langle -0.45, -0.74, 0.32 \rangle \] as the desired unit normal vector.
To find the equation for the normal plane, we do not actually need this normal vector. Since the normal plane is the plane orthogonal to the tangent vector (any tangent vector, not just the unit tangent -- only the direction matters), we can write down the equation immediately as the plane through the point \(\vec r(2) = \langle 2,4,8\rangle\) orthogonal to the vector \(T(2) = \langle 1,4,12\rangle\), yielding the equation \[ (x-2)+4(y-4)+12(z-8)=0. \]
Visualizing the Example
Shown below is the normal plane (as well as the full TNB frame) of the curve at \(t=2\):
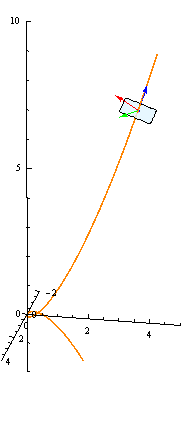
Further Questions
- In the image of the example above, which vector is the unit tangent, which is the unit normal, and which is the binormal vector?
- With \(\vec r(t)\) as in the example, are there any times \(t\) when \(\vec r'(t) = \vec T(t)\)? (Note that this is impossible to see graphically from the image above. Why?)
- In the Key Concepts animations above, the vectors generally vary smoothly as we sweep through the curve, but sometimes they jump suddenly. Why does this occur?
- In general, if \(\vec r(t)\) is unit speed, why is \(\vec r'(t)\) always orthogonal to \(\vec r(t)\)?
- We remarked above that \(\vec B(t) = \vec T(t)\times \vec N(t)\) is automatically a unit vector because \(\vec T(t)\) and \(\vec N(t)\) are orthogonal unit vectors. Give an example of two vectors \(\vec v\) and \(\vec u\) which are orthogonal, but where \(\vec v\times\vec u\) is not a unit vector. Then give a different example of two vectors \(\vec v\) and \(\vec u\) which are unit vectors, but where \(\vec v\times\vec u\) is not a unit vector.
- We also said that for any time \(t=t_0\), because the TNB frame is an orthonormal basis, we can write any vector \(\vec v\) in terms of its TNB components \[ \vec v = (\vec v\cdot \vec T(t_0)) \vec T(t_0) + (\vec v\cdot \vec N(t_0)) \vec N(t_0) + (\vec v\cdot \vec B(t_0)) \vec B(t_0). \] Consider the vectors \[\begin{aligned} \vec e_1 &= \langle 1, 0, 0\rangle \\ \vec e_2 &= \langle 1, 1, 0\rangle \\ \vec e_3 &= \langle 1, 1, 1\rangle, \end{aligned}\] and let \(\vec v = \langle 2, 0, -3 \rangle\). Note that \(\vec e_1\), \(\vec e_2\), and \(\vec e_3\) are not orthogonal, and \(\vec e_2\) and \(\vec e_3\) are not unit vectors. Is it still true that \[ \vec v = (\vec v\cdot \vec e_1)\vec e_1 + (\vec v\cdot \vec e_2)\vec e_2 + (\vec v\cdot \vec e_3)\vec e_3? \] Is it possible to find constants \(a\), \(b\), and \(c\) so that \[ \vec v = a\vec e_1 + b\vec e_2 + c\vec e_3? \]
Using the Mathematica Demo
All graphics on this page were generated by the Mathematica notebook 13_3TNBFrames.nb.
This notebook generates images and animations like those on this page for any curve.
As an exercise, use the notebook to provide a visual demonstration illustrating your answer to Question 2.
Investigate other curves \(\vec r(t)\) and their TNB frames. We have already defined the normal plane as the plane in which both the unit normal and binormal vectors lie. There are two other planes defined by the TNB frame. What do they look like? (The plane in which both the unit tangent and unit normal vectors lie is often called the osculating plane.)