Key Concepts
Average Rate of Change
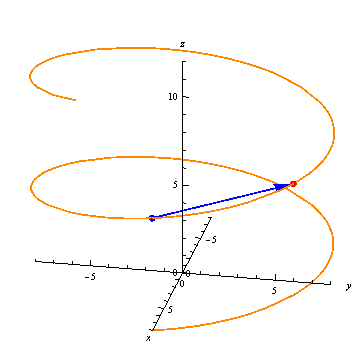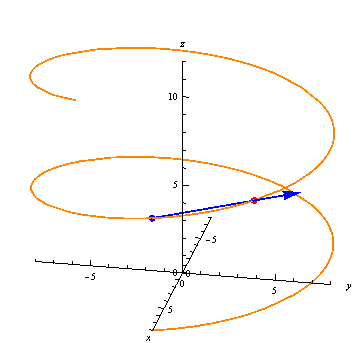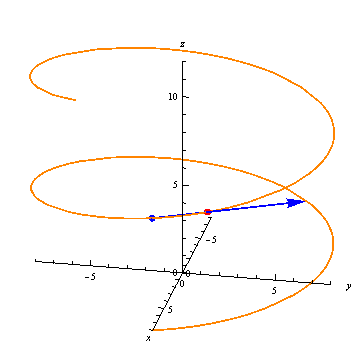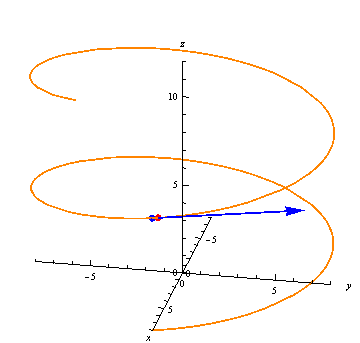
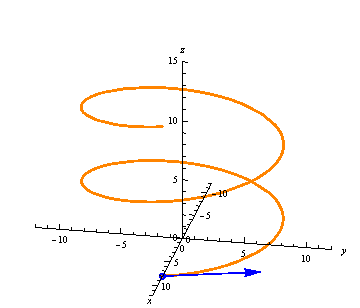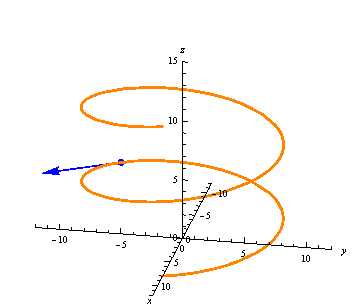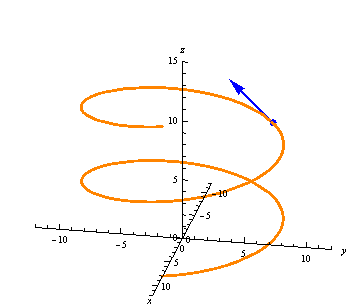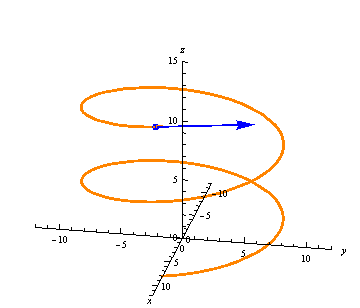
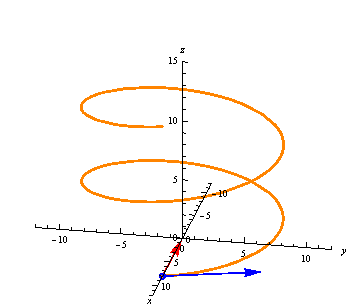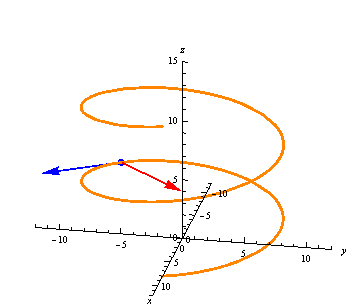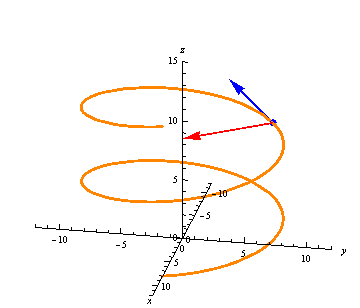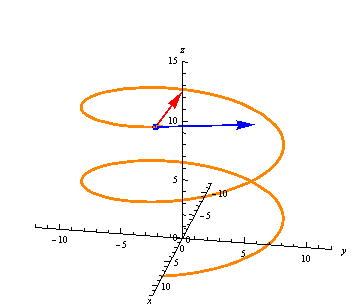
Let \(\vec r(t)\) be a vector-valued function. Just as in single-variable calculus, we can calculate the average rate of change between two points \(t=t_1\) and \(t=t_2\) as the difference quotient \[ \frac{\vec r(t_2) - \vec r(t_1)}{t_2-t_1}. \] Note that \(\vec r(t_2) - \vec r(t_1)\) is the vector from \(\vec r(t_1)\) to \(\vec r(t_2)\), so the average rate of change is just this vector divided by the scalar \(t_2-t_1\). Hence the average rate of change points from \(\vec r(t_1)\) to \(\vec r(t_2)\):
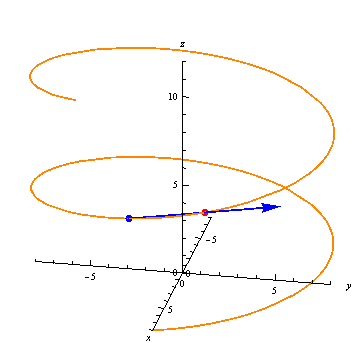
The average rate of change may be longer or shorter than this distance, though, depending on the difference \(t_2-t_1\).
Again following single-variable calculus, we can define the derivative as a limit of average rates of change:
The derivative of \(\vec r(t)\) is \[ \vec r'(t) = \lim_{h\to 0}\frac{\vec r(t+h) - \vec r(t)}{h}, \] provided this limit exists.
We can see the average rates of change approaching the derivative at a point in the following animation:
The derivative gives us a vector at every point, always tangent to the curve:
Once we have the first derivative, we can repeat the process finding the second derivative \(\vec r''(t)\):
We can similarly define third and higher derivatives as well, though we tend to use first and second derivatives more often.
Illustrated Example
Find an equation for the line tangent to the curve \(\vec r(t) = \langle t^2, 3-t^2, t^3 \rangle\) at \(t=1\).
Worked Solution
The tangent line will pass through \(\vec r(1) = \langle 1, 2, 1\rangle\) and point in the direction of \(\vec r'(1)\). To find derivatives symbolically, we can simply differentiate \(\vec r(t)\) component-by-component. So we compute \[ \vec r'(t) = \langle 2t, -2t, 3t^2 \rangle \] so that \(\vec r'(1) = \langle 2, -2, 3\rangle.
The desired line is therefore \[\begin{aligned} \vec L(t) &= \vec r(1) + t\vec r'(1) \\ &= \langle 1, 2, 1 \rangle + t\langle 2, -2, 3\rangle \\ &= \langle 1+2t, 2-2t, 1+3t \rangle. \end{aligned}\]
Visualizing the Example
Shown below is the curve with its derivative vector at \(t=1\):
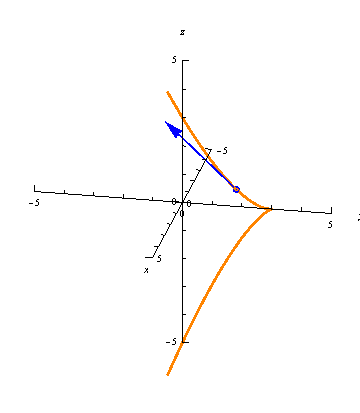
The tangent line is just the continuation of this derivative vector in both directions:

Further Questions
- In the image of the example above, we see that the curve has a sharp corner at a point. What point is this? Is the derivative defined at this point? Does it have a tangent line at this point?
- The first image in Key Concepts shows the average rate of change at a point. Based on the image, what can you say about \(\Delta t = t_2-t_1\)?
- What does the average rate of change look like when \(\Delta t=1\)?
-
The animation below shows a curve
and the derivatives of two different parameterizations
\(\vec r(t)\) and \(\vec s(t) = \vec r(at)\)
for some constant \(a > 1\):
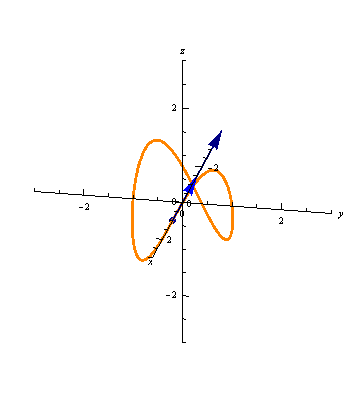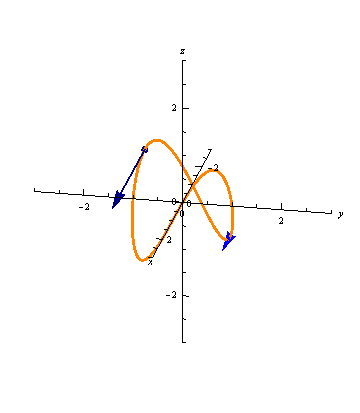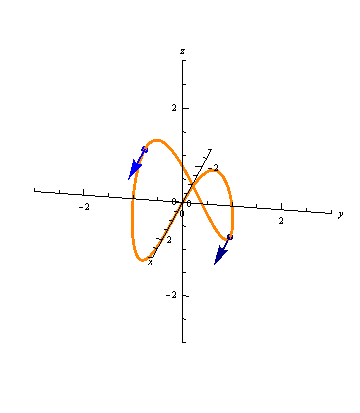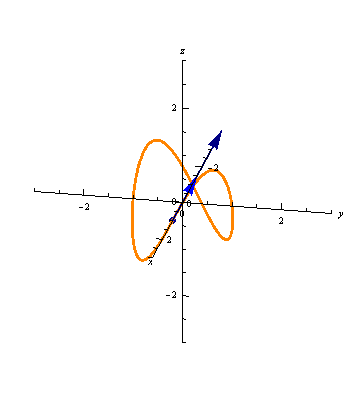
Which of the vectors are the derivatives of \(\vec r(t)\) and which are the derivatives of \(\vec s(t)\)? Estimate the value of \(a\).
Using the Mathematica Demo
All graphics on this page were generated by the Mathematica notebook 13_2DerivativesOfVectorValuedFunctions.nb.
This notebook generates images and animations like those on this page for any curve.
As an exercise, use the notebook to provide a visual demonstration illustrating your answer to Question 3.
Investigate other curves \(\vec r(t)\) and their derivatives. Find several examples of curves and points where \(\vec r'(t)=0\). Can you find examples that look smooth at that point? Can you find examples with a sharp corner at that point?